
- 문제
https://www.acmicpc.net/problem/2240
2240번: 자두나무
자두는 자두를 좋아한다. 그래서 집에 자두나무를 심어두고, 여기서 열리는 자두를 먹고는 한다. 하지만 자두는 키가 작아서 자두를 따먹지는 못하고, 자두가 떨어질 때까지 기다린 다음에 떨어
www.acmicpc.net
- 문제 풀이
- T(시간) : 1 ~ 1,000
- w(이동 가능 횟수) : 1 ~ 30
어떠한 특정 상황에서 자두를 줍기 위해 행동할 수 있는 경우를 모두 생각해보자.
- 현재 위치에 자두가 떨어지는 경우
자리를 바꿔 자두를 줍지 않는다.- 자리를 바꾸지 않고 자두를 줍는다.
- 현재 위치가 아닌 곳에 자두가 떨어지는 경우
- 자리를 바꿔 자두를 줍는다.
- 자리를 바꾸지 않고 자두를 줍는다.
총 4가지의 경우의 수가 있지만, 굳이 자기 자리에 자두가 떨어지는데 줍지 않고 자리를 바꿀 이유가 없다.
만약 이를 완전탐색을 통해 모든 경우의 수를 찾으려고 한다면 최악의 경우 21000 정도이다. 따라서 시간 복잡도를 개선할 필요성이 있다.
그리디...? 이 문제에서는 매초마다 최선의 선택을 하면서 행동을 하는 경우는 최적해를 보장하지 못한다. 다음을 살펴보자.
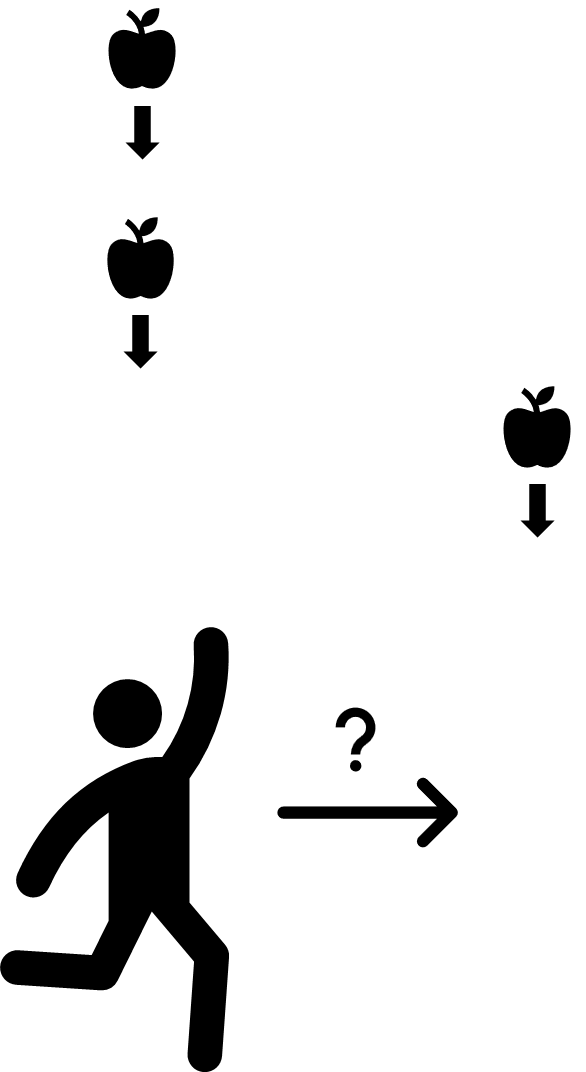
위 그림과 같은 상황에서 바로 당장을 위해서는 이동해 자두를 줍는 것이 좋겠지만 그 뒤로 떨어지는 자두는 모두 원래의 위치에 떨어지기 때문에 결과적으로 손해를 보게 된다. 그럼 이렇게 전부 계산해보기에는 너무 계산량이 많고, 그렇다고 최선의 상황을 선택하는 것이 최적해를 보장해주지 않는 상황에서는 어떻게 문제를 해결해야할까?
DP와 메모이제이션을 통한 반복적인 계산을 줄이기를 통해 해결할 수 있다. 이를 위해서는 현재 상태를 나타낼 수 있는 변수와 차원을 결정해야 한다.
현재 위치, 남은 이동 횟수, 현재 시간 = 현재까지 주운 자두의 최대 개수
이를 수식으로 표현하면 다음과 같다.
DP[pos][cnt][time] = value
이렇게 표현한 수식을 통해 점화식을 구하면 다음과 같다.
- 현재 위치에 자두가 떨어지는 경우
- 자리를 바꾸지 않음 : DP[pos][cnt][time+1] = DP[pos][cnt][time] + 1
- 현재 위치가 아닌 곳에 자두가 떨어지는 경우
- 자리를 바꿈 : DP[nextPos][cnt-1][time+1] = max(DP[nextPos][cnt-1][time+1], DP[pos][cnt][time+1] + 1)
- 자리를 안바꿈 : DP[pos][cnt][time+1] = DP[pos][cnt][time]
이러한 점화식이 어떻게 작동하는지 그림으로 한번 살펴보자.
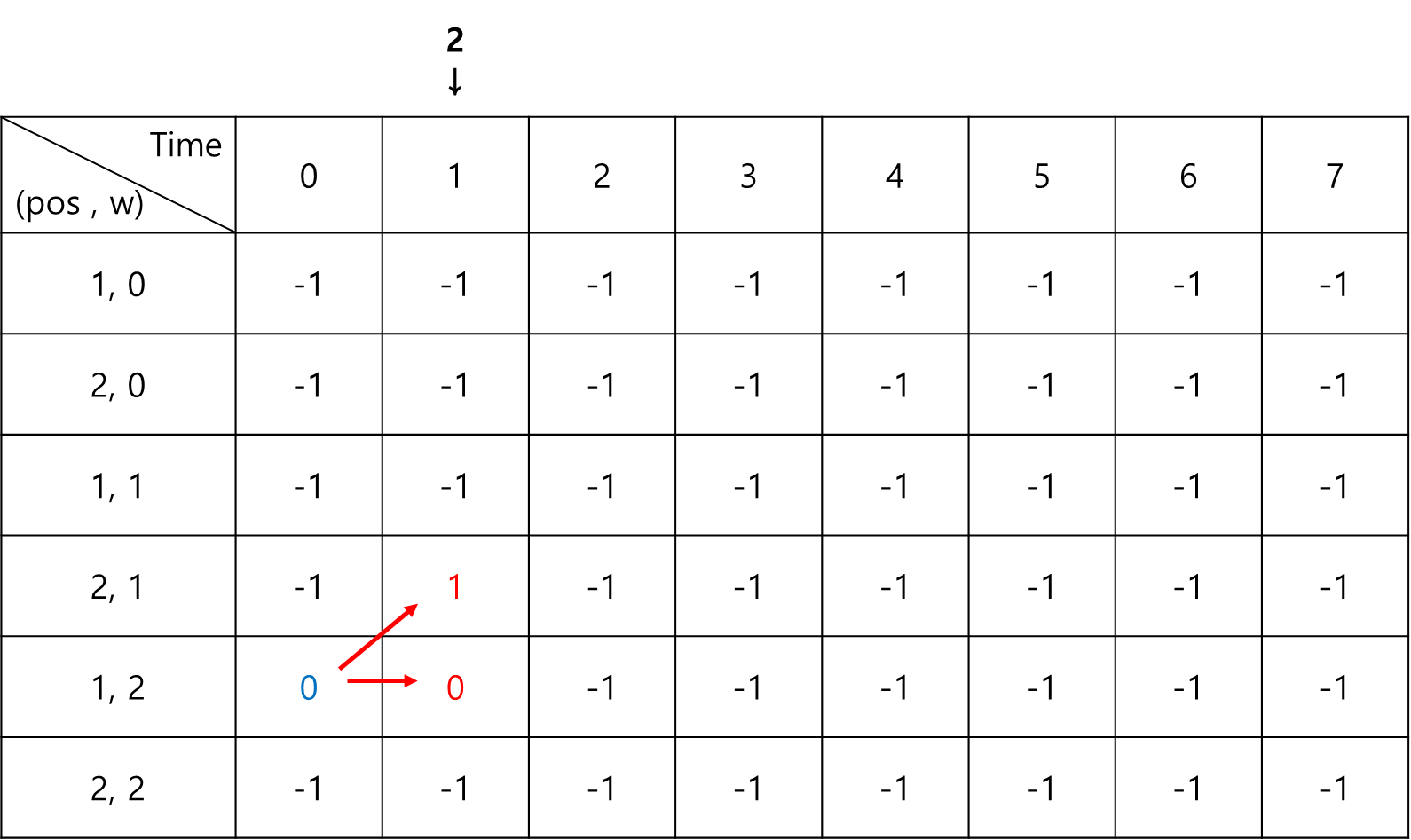
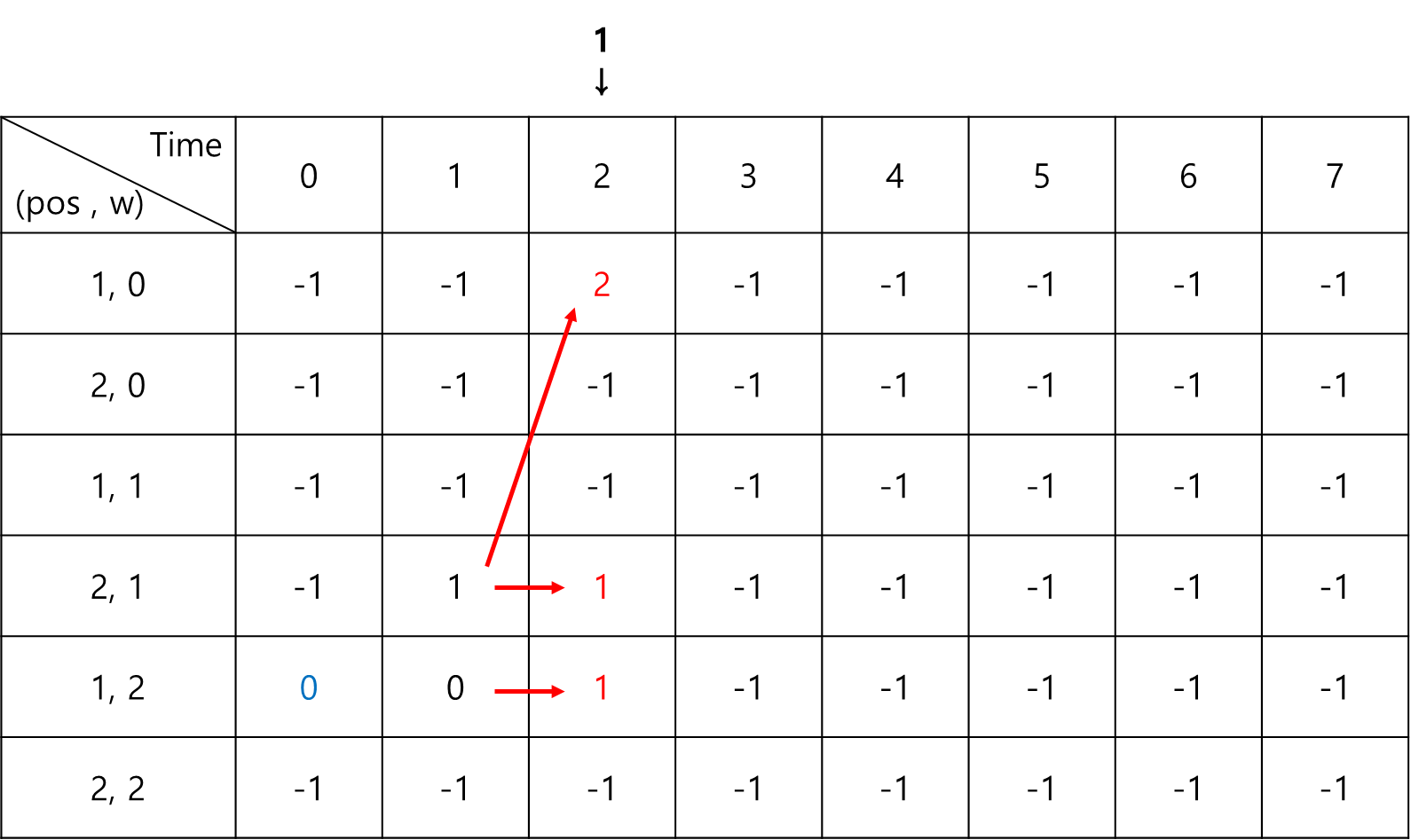
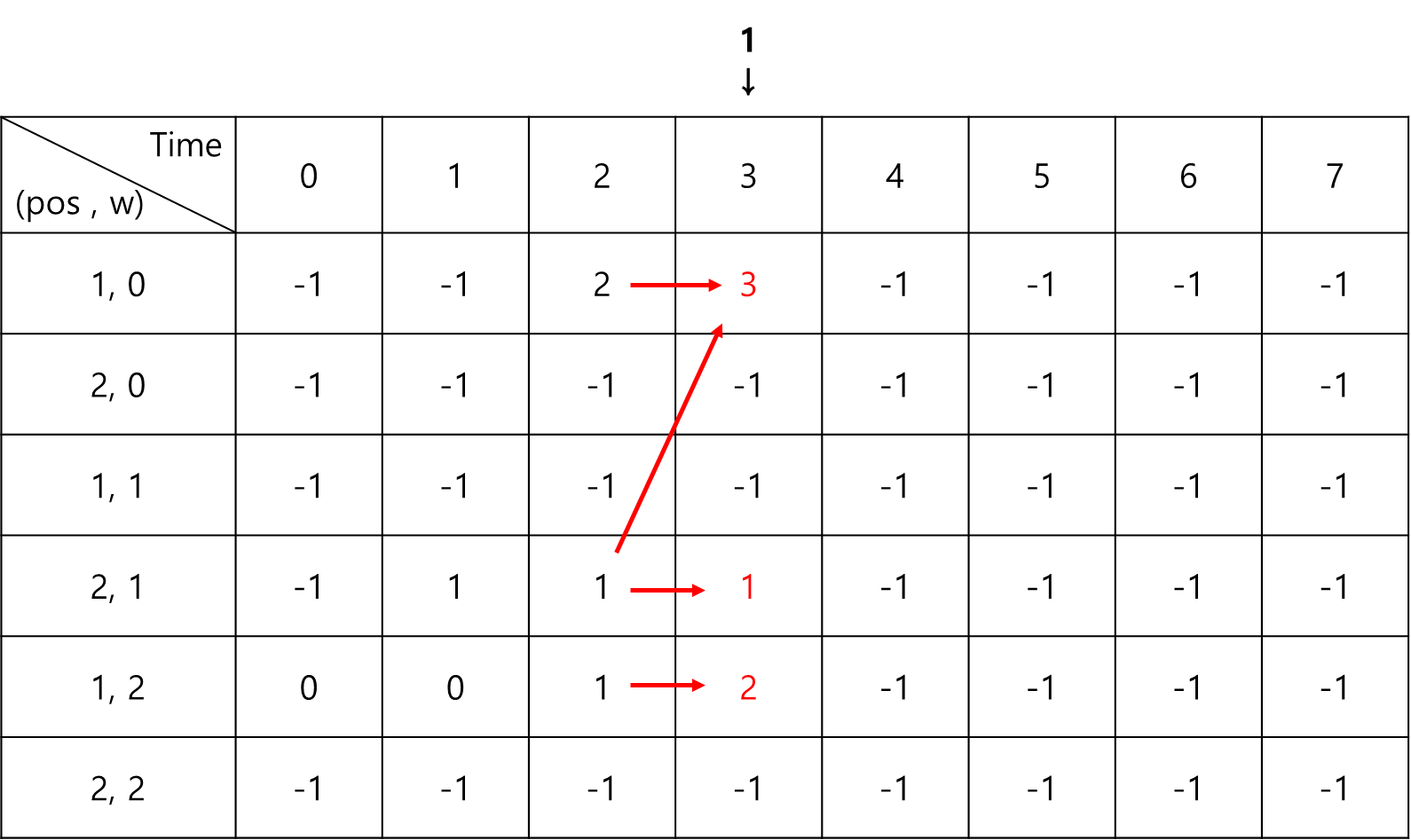

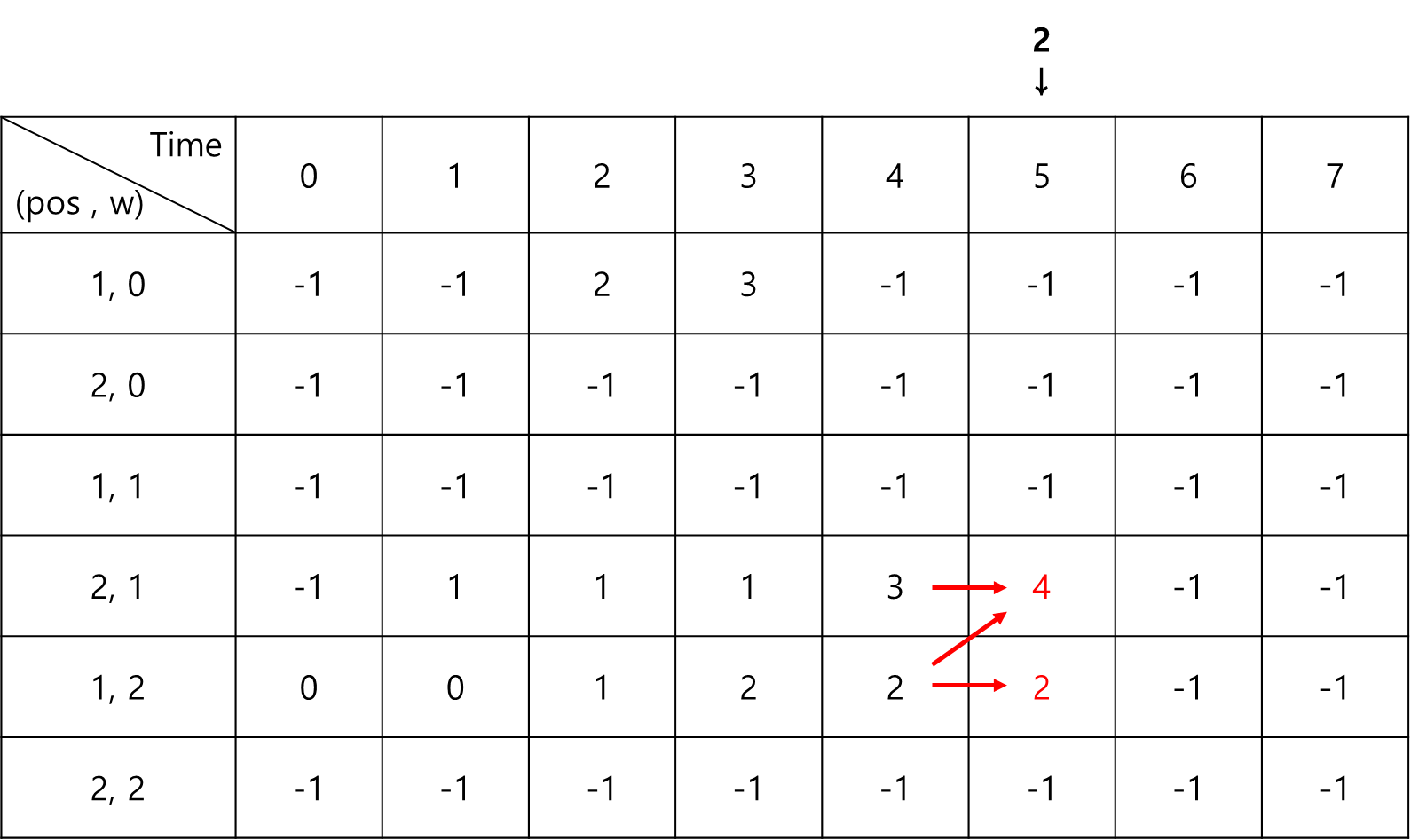
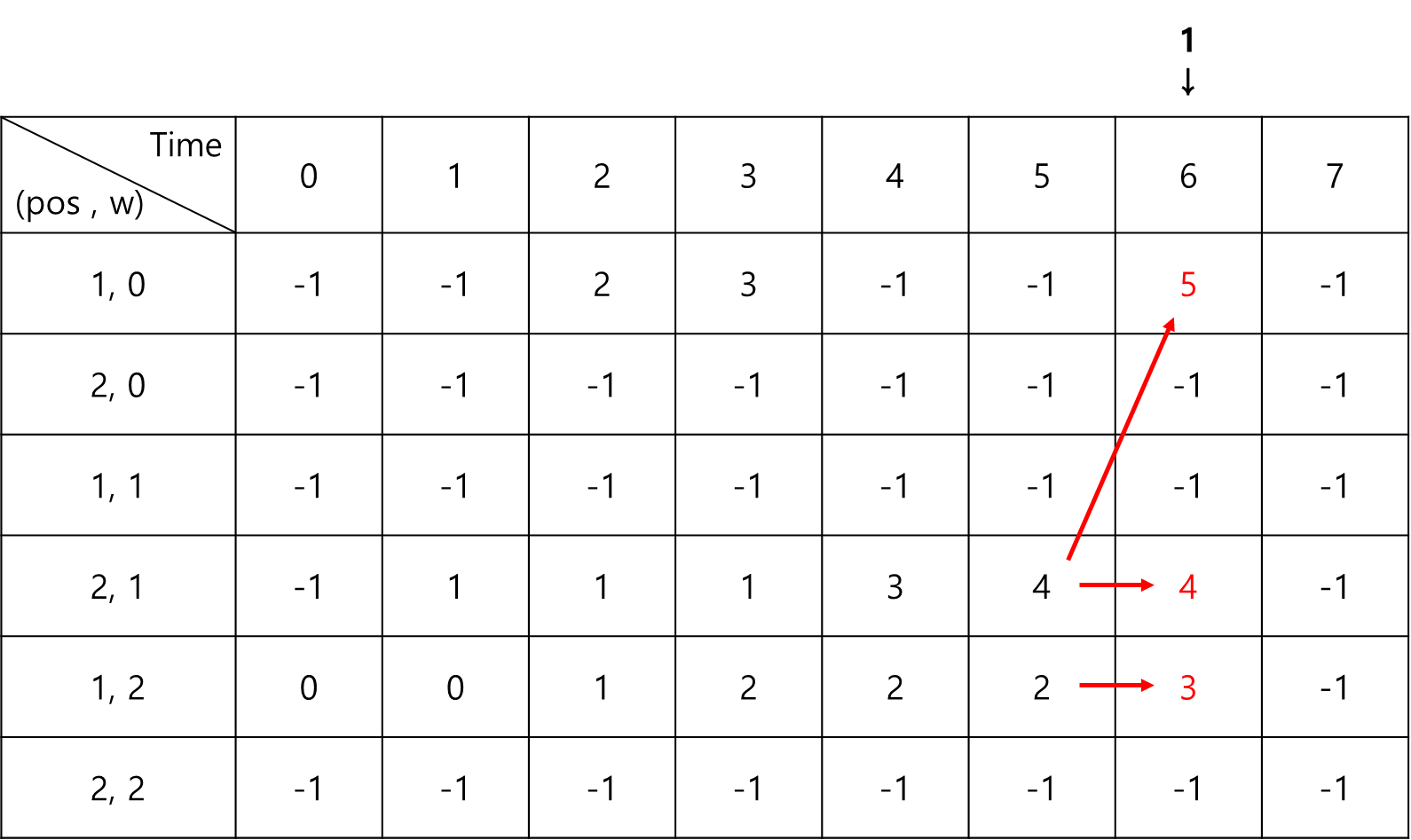
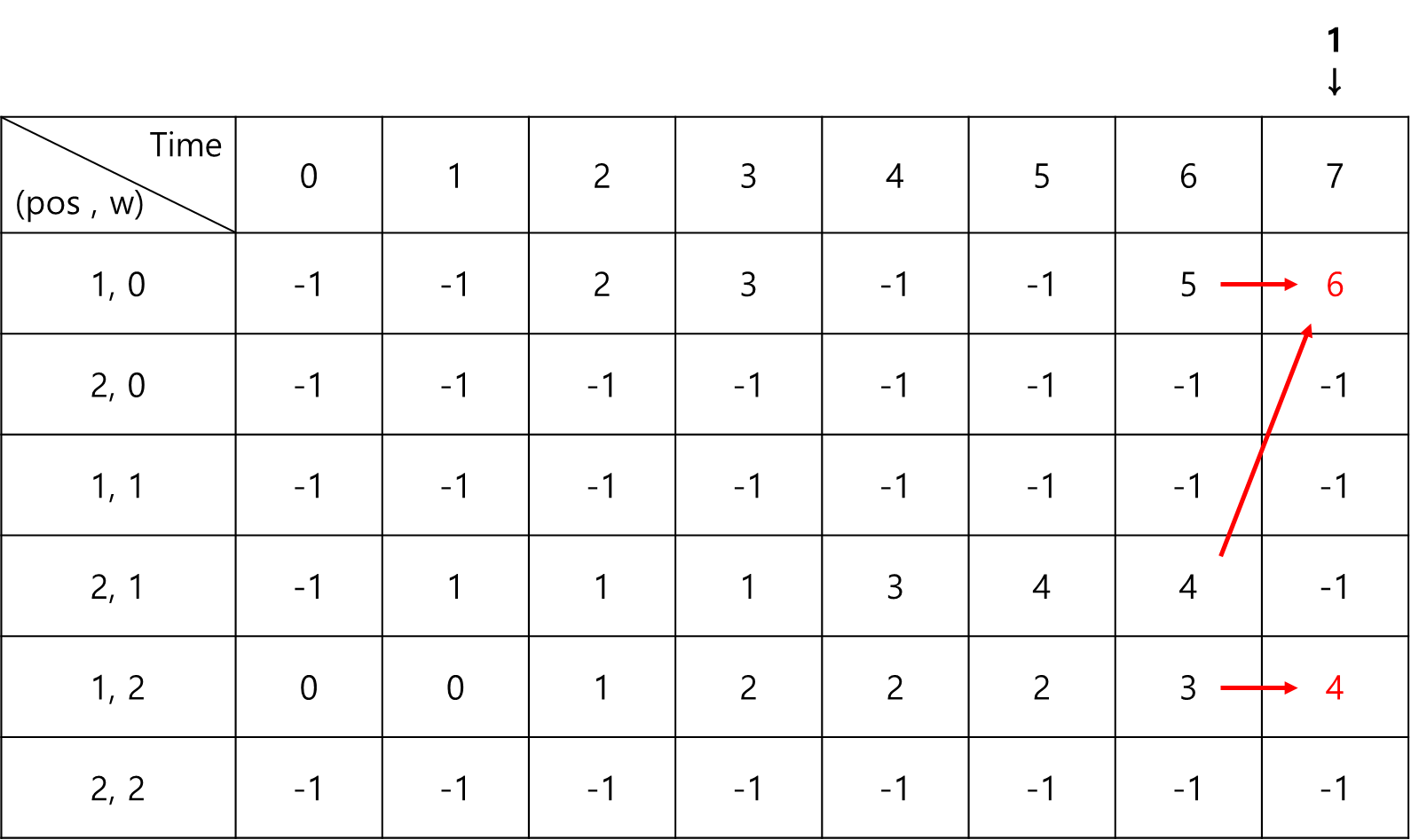
점화식을 다 수행하고 나서 배열 안의 최댓값을 찾으면 최적해가 된다.
- 코드
#include <bits/stdc++.h>
#define fastio ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using namespace std;
int t, w, ans = 0;
int dropOrder[1001];
int dp[3][31][1001];
// dp[현재위치][남은움직임횟수][현재시간] = 현재 가진 최대 자두 개수
void init() {
// 입력
cin >> t >> w;
for (int i = 1; i <= t; i++) {
cin >> dropOrder[i];
}
memset(dp, -1, sizeof(dp));
}
int solve() {
dp[1][w][0] = 0;
for (int time = 0; time < t; time++) {
for (int cnt = 0; cnt <= w; cnt++) {
for (int pos = 1; pos <= 2; pos++) {
if (dp[pos][cnt][time] >= 0) {
int nextPos = dropOrder[time + 1];
if (pos == nextPos) { // 현재 위치에 자두가 떨어짐
dp[pos][cnt][time + 1] = dp[pos][cnt][time] + 1;
}
else { // 현재 위치에 자두가 떨어지지 않음
if (cnt != 0) { // 움직여서 자두를 줍는 경우
dp[nextPos][cnt - 1][time + 1] = max(dp[nextPos][cnt - 1][time + 1], dp[pos][cnt][time] + 1);
} // 움직이지 않는 경우
dp[pos][cnt][time + 1] = dp[pos][cnt][time];
}
};
}
}
}
// w를 모두 소모해서 더이상 움직이지 못하는 경우와 시간이 t인 경우를 모두 비교
int ret = 0;
for (int pos = 1; pos <= 2; pos++) {
for (int time = 1; time <= t; time++) {
ret = max(ret, dp[pos][0][time]);
}
for (int i = 0; i <= w; i++) {
ret = max(ret, dp[pos][i][t]);
}
}
return ret;
}
int main() {
fastio;
init();
cout << solve();
return 0;
}

- 문제
https://www.acmicpc.net/problem/2240
2240번: 자두나무
자두는 자두를 좋아한다. 그래서 집에 자두나무를 심어두고, 여기서 열리는 자두를 먹고는 한다. 하지만 자두는 키가 작아서 자두를 따먹지는 못하고, 자두가 떨어질 때까지 기다린 다음에 떨어
www.acmicpc.net
- 문제 풀이
- T(시간) : 1 ~ 1,000
- w(이동 가능 횟수) : 1 ~ 30
어떠한 특정 상황에서 자두를 줍기 위해 행동할 수 있는 경우를 모두 생각해보자.
- 현재 위치에 자두가 떨어지는 경우
자리를 바꿔 자두를 줍지 않는다.- 자리를 바꾸지 않고 자두를 줍는다.
- 현재 위치가 아닌 곳에 자두가 떨어지는 경우
- 자리를 바꿔 자두를 줍는다.
- 자리를 바꾸지 않고 자두를 줍는다.
총 4가지의 경우의 수가 있지만, 굳이 자기 자리에 자두가 떨어지는데 줍지 않고 자리를 바꿀 이유가 없다.
만약 이를 완전탐색을 통해 모든 경우의 수를 찾으려고 한다면 최악의 경우 21000 정도이다. 따라서 시간 복잡도를 개선할 필요성이 있다.
그리디...? 이 문제에서는 매초마다 최선의 선택을 하면서 행동을 하는 경우는 최적해를 보장하지 못한다. 다음을 살펴보자.

위 그림과 같은 상황에서 바로 당장을 위해서는 이동해 자두를 줍는 것이 좋겠지만 그 뒤로 떨어지는 자두는 모두 원래의 위치에 떨어지기 때문에 결과적으로 손해를 보게 된다. 그럼 이렇게 전부 계산해보기에는 너무 계산량이 많고, 그렇다고 최선의 상황을 선택하는 것이 최적해를 보장해주지 않는 상황에서는 어떻게 문제를 해결해야할까?
DP와 메모이제이션을 통한 반복적인 계산을 줄이기를 통해 해결할 수 있다. 이를 위해서는 현재 상태를 나타낼 수 있는 변수와 차원을 결정해야 한다.
현재 위치, 남은 이동 횟수, 현재 시간 = 현재까지 주운 자두의 최대 개수
이를 수식으로 표현하면 다음과 같다.
DP[pos][cnt][time] = value
이렇게 표현한 수식을 통해 점화식을 구하면 다음과 같다.
- 현재 위치에 자두가 떨어지는 경우
- 자리를 바꾸지 않음 : DP[pos][cnt][time+1] = DP[pos][cnt][time] + 1
- 현재 위치가 아닌 곳에 자두가 떨어지는 경우
- 자리를 바꿈 : DP[nextPos][cnt-1][time+1] = max(DP[nextPos][cnt-1][time+1], DP[pos][cnt][time+1] + 1)
- 자리를 안바꿈 : DP[pos][cnt][time+1] = DP[pos][cnt][time]
이러한 점화식이 어떻게 작동하는지 그림으로 한번 살펴보자.


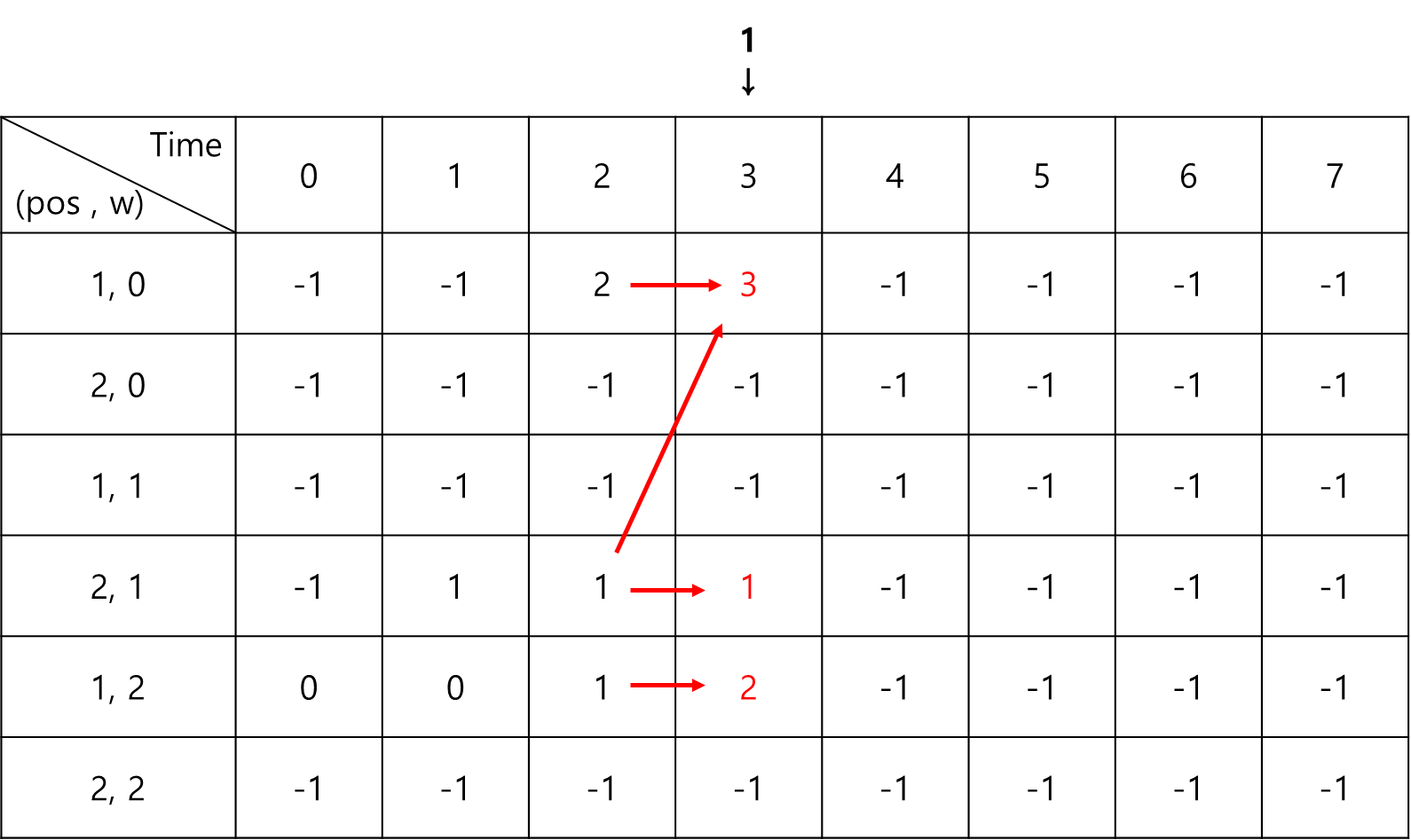

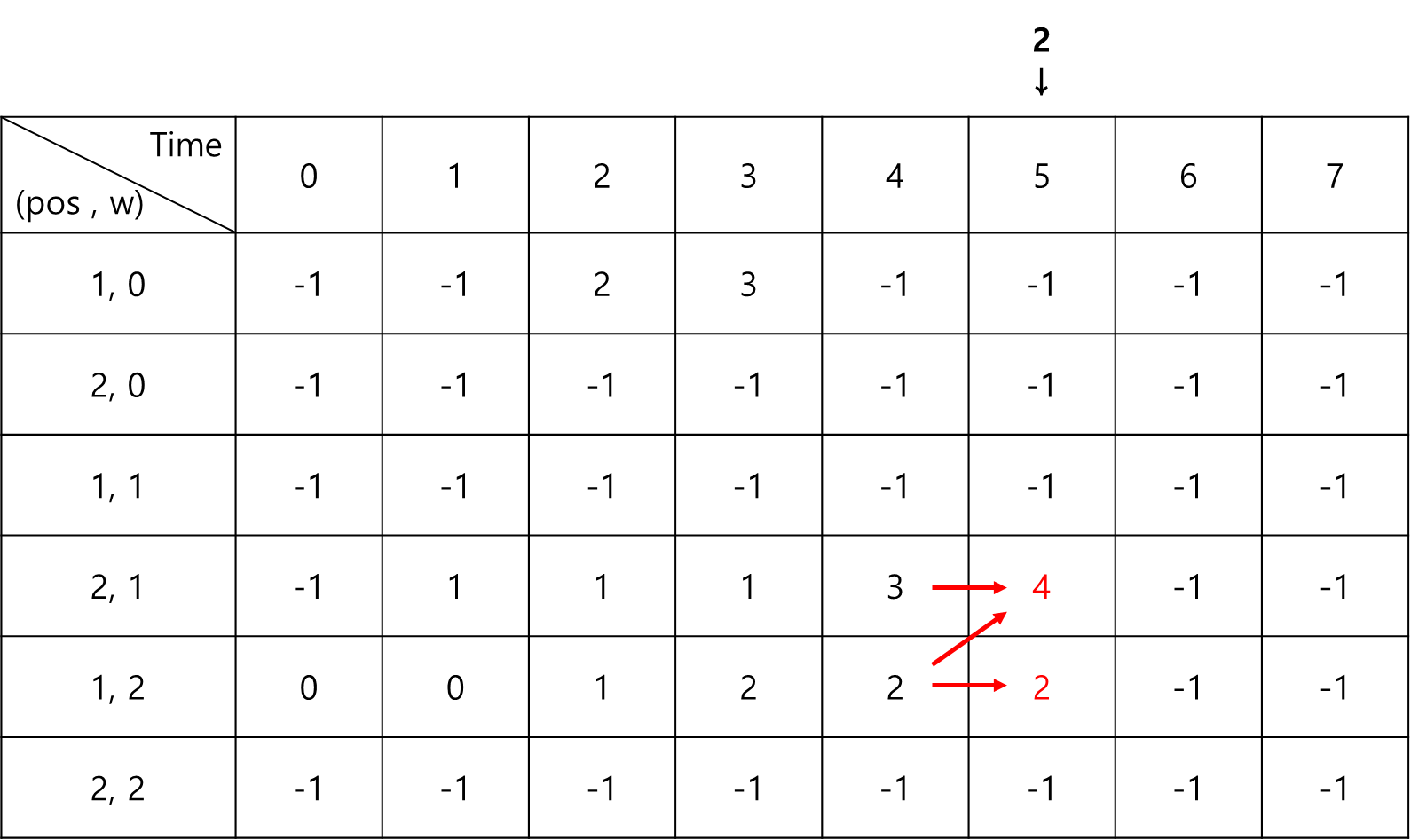
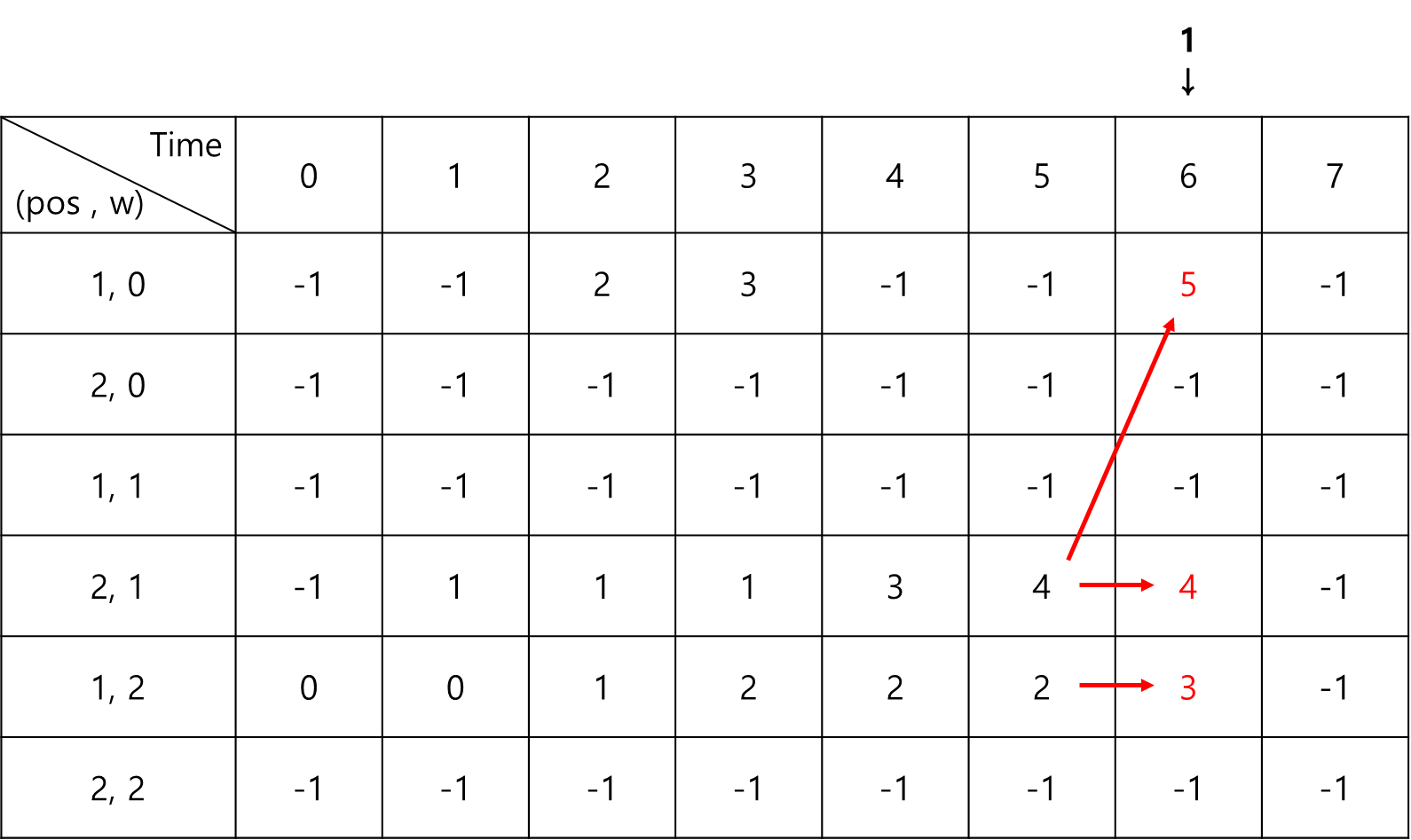

점화식을 다 수행하고 나서 배열 안의 최댓값을 찾으면 최적해가 된다.
- 코드
#include <bits/stdc++.h>
#define fastio ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using namespace std;
int t, w, ans = 0;
int dropOrder[1001];
int dp[3][31][1001];
// dp[현재위치][남은움직임횟수][현재시간] = 현재 가진 최대 자두 개수
void init() {
// 입력
cin >> t >> w;
for (int i = 1; i <= t; i++) {
cin >> dropOrder[i];
}
memset(dp, -1, sizeof(dp));
}
int solve() {
dp[1][w][0] = 0;
for (int time = 0; time < t; time++) {
for (int cnt = 0; cnt <= w; cnt++) {
for (int pos = 1; pos <= 2; pos++) {
if (dp[pos][cnt][time] >= 0) {
int nextPos = dropOrder[time + 1];
if (pos == nextPos) { // 현재 위치에 자두가 떨어짐
dp[pos][cnt][time + 1] = dp[pos][cnt][time] + 1;
}
else { // 현재 위치에 자두가 떨어지지 않음
if (cnt != 0) { // 움직여서 자두를 줍는 경우
dp[nextPos][cnt - 1][time + 1] = max(dp[nextPos][cnt - 1][time + 1], dp[pos][cnt][time] + 1);
} // 움직이지 않는 경우
dp[pos][cnt][time + 1] = dp[pos][cnt][time];
}
};
}
}
}
// w를 모두 소모해서 더이상 움직이지 못하는 경우와 시간이 t인 경우를 모두 비교
int ret = 0;
for (int pos = 1; pos <= 2; pos++) {
for (int time = 1; time <= t; time++) {
ret = max(ret, dp[pos][0][time]);
}
for (int i = 0; i <= w; i++) {
ret = max(ret, dp[pos][i][t]);
}
}
return ret;
}
int main() {
fastio;
init();
cout << solve();
return 0;
}
